14.2 Two-Samples: Hypothesis Testing on the Difference in Proportions
Comparing two proportions is often necessary to see if they are significantly different from each other. For example, suppose you do a randomized control study on 40 people, half assigned to a treatment and other half assigned to a placebo. 18/20 from the experiment group got better, while 15/20 from the control group also got better. Are these two proportions significantly different from each other? Is the treatment effective?13
We are interested in testing the hypotheses:
\[H_0: p_1=p_2\]
\[H_1: p_1 \neq p_2\]
If the null hypothesis \(H_0: p_1=p_2\) is true, using the fact that \(p_1=p_2=p,\) the random variable
\[ Z=\dfrac{(\hat{p_1}-\hat{p_2})}{\sqrt{\hat{p}(1-\hat{p}) \left( \dfrac{1}{n_1} +\dfrac{1}{n_2}\right) } }\]
has approximately a standard normal distribution, \(N(0,1)\).
Where \(\hat{p_1}=x_1/n_1\) $=x_2/n_2 $ and the estimator of the common \(p\), or pooled sample proportion, is:
\[\hat{p}=\dfrac{x_1+x_2}{n_1+n_2}\] \[\hat{p}=\dfrac{p_1n_1+p_2n_2}{n_1+n_2}\]
14.2.1 The Hypotheses and \(p\)-value
The null hypothesis is our statement of no effect. In this case our null hypothesis is that there is no difference between the two population proportions. We can write this as \(H_0: p_1 = p_2\).14
The alternative hypothesis is one of three possibilities, depending upon the specifics of what we are testing for:
- \(H_1\): \(p_1\) is greater than \(p_2\).
- This is a one-tailed or one-sided test.
- Equivalent to: \(H_1: p_1 - p_2 > 0\)
- \(p\)-value is the proportion of the normal distribution that is greater than Z.
- \(H_1\): \(p_1\) is less than \(p_2\).
- This is also one-sided test.
- Equivalent to: \(H_1: p_1 - p_2 < 0\)
- \(p\)-value is the proportion of the normal distribution that is less than Z.
- \(H_1\): \(p_1\) is not equal to \(p_2\).
- This is a two-tailed or two-sided test.
- Equivalent to: \(H_1: p_1 - p_2 \neq 0\)
- \(p\)-value is the the proportion of the normal distribution that is greater than \(|Z|\), the absolute value of \(Z\).
14.2.2 Decision rule
Now we make a decision on whether to reject the null hypothesis (and thereby accept the alternative), or to fail to reject the null hypothesis. We make this decision by comparing our p-value to the level of significance \(\alpha\).
If the \(p\)-value is less than or equal to \(\alpha\), then we reject the null hypothesis. This means that we have a statistically significant result and that we are going to accept the alternative hypothesis.
If the \(p\)-value is greater than \(\alpha\), then we fail to reject the null hypothesis. This does not prove that the null hypothesis is true. Instead it means that we did not obtain convincing enough evidence to reject the null hypothesis.
14.2.3 Example 01
Suppose the Acme Drug Company develops a new drug, designed to prevent colds. The company states that the drug is equally effective for men and women. To test this claim, they choose a a simple random sample of \(100\) women and \(200\) men from a population of \(100,000\) volunteers.
At the end of the study, \(38\%\) of the women caught a cold; and \(51\%\) of the men caught a cold. Based on these findings, can we reject the company’s claim that the drug is equally effective for men and women? Use a \(0.05\) level of significance.
From here
Data
\[ \hat{p_1}=0.38; \,\,\, \hat{p_2}=0.51; \,\,\, n_1=100 \,\,\, n_2=200 \]
Hypothesis
\[H_0: p_1 = p_2\] \[H_1: p_1 \neq p_2\]
t-stat
\[\hat{p}=\dfrac{0.38 \times 100 + 0.51 \times 200}{100+200}=0.467\]
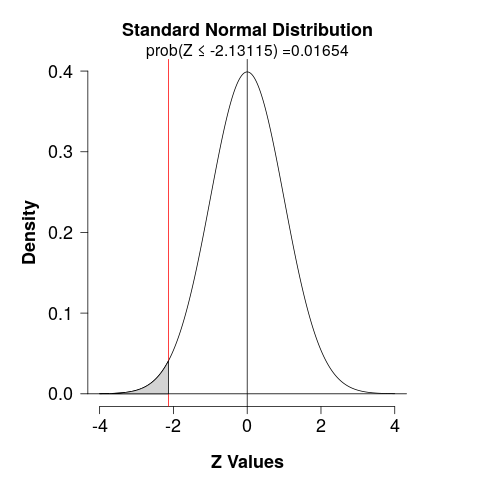
\[ Z=\dfrac{(0.38-0.51)}{\sqrt{0.467 \times (1-0.467) \times \left( \dfrac{1}{100} +\dfrac{1}{200}\right) } } = \dfrac{-0.13}{0.061} = -2.13115\]
p-value
<div class=“column_2 style=”padding:20px;">
- The \(p\)-value is the probability of being less or greater than 2.13 is \(P(z < -2.13115) = 0.01659\), and \(P(z > 2.13115) = 0.01659\).
- Thus, the \(p\)-value = \(0.01654 + 0.01654 = 0.03308\).
- Since \(p\)-value is just less than \(0.05\), we have enough evidence to reject \(H_0\).
Conclusion
Since the \(p\)-value (\(0.034\)) is less than the significance level (\(\alpha =0.05\)), we cannot accept the null hypothesis.
Suppose the previous example is stated a little bit differently. Suppose the Acme Drug Company develops a new drug, designed to prevent colds. The company states that the drug is more effective for women than for men. To test this claim, they choose a a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
At the end of the study, \(38\%\) of the women caught a cold; and \(51\%\) of the men caught a cold. Based on these findings, can we conclude that the drug is more effective for women than for men? Use a 0.01 level of significance.